DC CIRCUIT ANALYSIS
Basic DC Theory
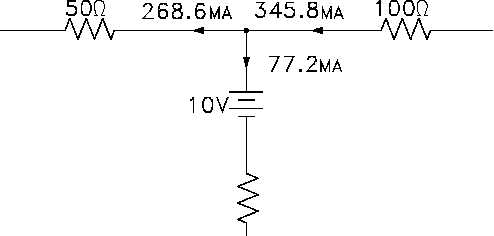
Figure 42 Applying Current Law to Junction
The sum of the currents out of the junction is:
0.2686 + 0.0772
=
0.3458 a
=
345.8 ma
The current into the junction is 345.8 ma.
The current into the junction is equal to the current out of the junction. Therefore, the solution
checks.
Node Equations
Kirchhoff’s current law, as previously stated, says that at any junction point in a circuit the
current arriving is equal to the current leaving. Let us consider five currents entering and leaving
a junction shown as P (Figure 43). This junction is also considered a node.
Assume that all currents entering the node are positive, and all currents that leave the node are
negative. Therefore, I1, I3, and I4 are positive, and I2 and I5 are negative. Kirchhoff’s Law also
states that the sum of all the currents meeting at the node is zero. For Figure 43, Equation
(2-19) represents this law mathematically.
I1 + I2 + I3 + I4 + I5 = 0
(2-19)
ES-02
Page 54
Rev. 0