INDUCTANCE
DC Circuits
The voltage drop across an inductor is directly proportional to the product of the inductance and
the time rate of change of current through the inductor, as shown in Equation (3-6).
VL
=
(3-6)
LDI
Dt
where
VL
=
voltage drop across the inductor (volts)
L
=
inductance (henries)
=
time rate of change of current (amp/sec)
DI
Dt
After five time constants, circuit parameters normally reach their final value. Circuits that
contain both inductors and resistors are called RL circuits. The following example will illustrate
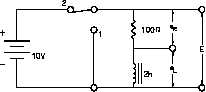
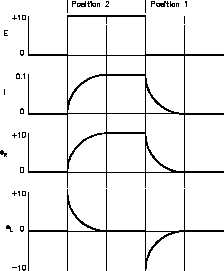
how an RL circuit reacts to changes in the circuit (Figure 8).
1.
Initially,
the
switch
is
in
Figure 8 Voltage Applied to an Inductor
Position 1, and no current flows
through the inductor.
2.
When we move the switch to
Position 2, the battery attempts to
force a current of 10v/100W =
0.1A through the inductor. But as
current
begins
to
flow,
the
inductor generates a magnetic
field. As the field increases, a
counter EMF is induced that
opposes the battery voltage. As a
steady state is reached, the counter
EMF goes to zero exponentially.
3.
When the switch is returned to
Position 1, the magnetic field
collapses, inducing an EMF that
tends to maintain current flow in
the same direction through the
inductor.
Its polarity will be
opposite to that induced when the
switch was placed in Position 2.
ES-03
Page 6
Rev. 0