Trigonometry
PYTHAGOREAN THEOREM
Rev. 0
Page 1
MA-04
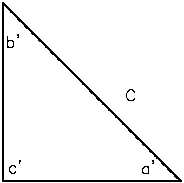
Figure 1 Triangle
PYTHAGOREAN THEOREM
This chapter covers right triangles and solving for unknowns using
the Pythagorean theorem.
EO 1.1
Given a problem, APPLY the Pythagorean theorem to
solve for the unknown values of a right triangle.
Trigonometry is the branch of mathematics that is the study of angles and the relationship
between angles and the lines that form them. Trigonometry is used in Classical Physics and
Electrical Science to analyze many physical phenomena. Engineers and operators use this
branch of mathematics to solve problems encountered in the classroom and on the job. The
most important application of trigonometry is the solution of problems involving triangles,
particularly right triangles.
Trigonometry is one of the most useful branches of mathematics. It is used to indirectly
measure distances which are difficult to measure directly. For example, the height of a flagpole
or the distance across a river can be measured using trigonometry.
As shown in Figure 1 below, a triangle is a plane figure
formed using straight line segments (AB, BC, CA) to
connect three points (A, B, C) that are not in a straight
line. The sum of the measures of the three interior
angles (a', b', c') is 180- , and the sum of the lengths of
any two sides is always greater than or equal to the
third.
Pythagorean Theorem
The Pythagorean theorem is a tool that can be used to
solve for unknown values on right triangles. In order to
use the Pythagorean theorem, a term must be defined.
The term hypotenuse is used to describe the side of a
right triangle opposite the right angle. Line segment C
is the hypotenuse of the triangle in Figure 1.
The Pythagorean theorem states that in any right triangle, the square of the length of the
hypotenuse equals the sum of the squares of the lengths of the other two sides.
This may be written as c = a + b or
.
(4-1)
2
2
2