'
Fx
T
1x
T
2x
T
3x
0
'
Fy
T
1y
T
2y
T
3y
0
'
Fy
(T1 sin30- )
(T2 sin180- )
(T3 sin270- )
0
(T1)(0.5)
(T2)(0)
(125 lbf)( 1)
0
0.5T1
125 lbf
0
0.5T1
125 lbf
T1
250 lbf
FORCE EQUILIBRIUM
Application of Newton's Laws
CP-04
Page 14
Rev. 0
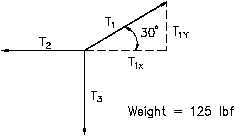
Figure 7 Free-Body Diagram
The tension in a cable is the force transmitted by the cable. The tension at any point in the cable
can be measured by cutting a suitable length from it and inserting a spring scale.
Solution:
Since the object and its supporting cables are motionless (i.e., in equilibrium), we know
that the net force acting on the intersection of the cables is zero. The fact that the net
force is zero tells us that the sum of the x-components of T , T , and T is zero, and the
1
2
3
sum of the y-components of T , T , and T is zero.
1
2
3
The tension T is equal to the weight of the object, 125 lbf. The x and y components of the
3
tensions can be found using trigonometry (e.g., sine function). Substituting known values into the
second equation above yields the following.
A simpler method to solve this problem involves assigning a sign convention to the free-body
diagram and examining the direction of the forces.