ANALYTICAL METHOD OF VECTOR ADDITION
Vectors
CP-02
Page 24
Rev. 0
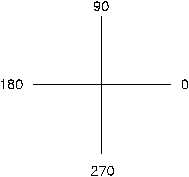
Figure 23 Trigonometric Functions
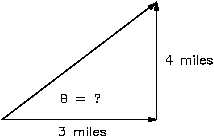
Figure 24 Hypotenuse and Angle
Also, recall the three trigonometric functions
reviewed in an earlier chapter and shown in
Figure 23. The cosine will be used to solve for
F . The sine will be used to solve for F .
x
y
Tangent will normally be used to solve for ,
although sine and cosine may also be used.
On a rectangular coordinate system, the sine
values of are positive (+) in quadrants I and II
and negative (-) in quadrants III and IV. The
cosine values of are positive (+) in quadrants
I and IV and negative (-) in quadrants II and III.
Tangent values are positive (+) in quadrants I
and III and negative (-) in quadrants II and IV.
When mathematically solving for tan , calculators will specify angles in quadrants I and IV only.
Actual angles may be in quadrants II and III. Each problem should be analyzed graphically to
report a realistic solution. Quadrant II and III angles may be obtained by adding or subtracting
180 from the value calculated.
o
Using the Analytical Method
To illustrate this method, consider this example: a man walks 3 miles in one direction, then turns
90 and continues to walk for an additional 4 miles. In what direction and how far is he from his
o
starting point? The first step in solving this problem is to draw a simple sketch as shown in Figure
24.