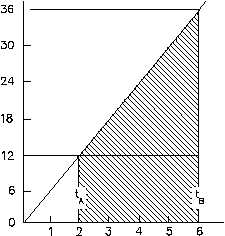
CALCULUS Higher Concepts of Mathematics The value of this integral can be determined for Figure 8     Graph of Velocity vs. Time the  case  plotted  in  Figure  8  by  noting  that  the velocity is increasing linearly.   Thus, the average velocity for the time interval between t_A and t_B is the  arithmetic  average  of  the  velocity  at  t_A  and the velocity at t_B.   At time t_A, v = 6t_A; at time t_B, v = 6t_B.   Thus, the average velocity for the time interval  between  t_A  and  t_B  is which                 6t_A       6t_B 2 equals 3(t_A + t_B).  Using this average velocity, the total    distance    traveled    in    the    time    interval between  t_A  and  t_B  is  the  product  of  the  elapsed time t_B - t_A and the average velocity 3(t_A + t_B). s = v_avDt s = 3(t_A + t_B)(t_B - t_A) (5-16) Equation 5-16 is also the value of the integral of the velocity, v, with respect to time, t, between the limits t_A -t_B for the case plotted in Figure 8. t_B t_A vdt      3(t_A       t_B)(t_B       t_A) The cross-hatched area in Figure 8 is the area under the velocity curve between  t = t_A and t = t_B.   The value of this area can be computed by adding the area of the rectangle whose sides are t_B - t_A and the velocity at t_A, which equals 6t_A - t_B, and the area of the triangle whose base is t_B - t_A and whose height is the difference between the velocity at  t_B and the velocity at  t_A, which equals 6t_B - t_A. Area      [(t_B       t_A)(6t_A)]   1 2 (t_B       t_A)(6t_b       6t_A) Area      6t_A t_B       6t²_A       3t²_B       6t_A t_B       3t²_A Area      3t²_B       3t²_A Area      3(t_B       t_A)(t_B       t_A) MA-05 Page 44 Rev. 0