Properties of Metals
DOE-HDBK-1017/1-93
STRAIN
When metal experiences strain, its volume remains constant. Therefore, if volume remains
constant as the dimension changes on one axis, then the dimensions of at least one other axis
must change also. If one dimension increases, another must decrease. There are a few
exceptions. For example, strain hardening involves the absorption of strain energy in the
material structure, which results in an increase in one dimension without an offsetting decrease
in other dimensions. This causes the density of the material to decrease and the volume to
increase.
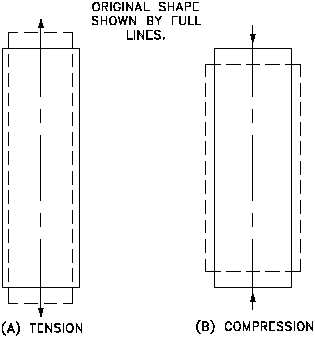
If a tensile load is applied to a material, the material will elongate on the axis of the load
(perpendicular to the tensile stress plane), as illustrated in Figure 2(a). Conversely, if the load
is compressive, the axial dimension will decrease, as illustrated in Figure 2(b). If volume is
constant, a corresponding lateral contraction or expansion must occur. This lateral change will
bear a fixed relationship to the axial strain. The relationship, or ratio, of lateral to axial strain
is called Poisson's ratio after the name of its discoverer. It is usually symbolized by n.
Whether or not a material can deform
Figure 2 Change of Shape of Cylinder Under Stress
plastically at low applied stresses depends
on its lattice structure. It is easier for
planes of atoms to slide by each other if
those
planes
are
closely
packed.
Therefore lattice structures with closely
packed planes
allow more plastic
deformation than those that are not closely
packed.
Also, cubic lattice structures
allow slippage to occur more easily than
non-cubic lattices. This is because of
their symmetry which provides closely
packed planes in several directions. Most
metals are made of the body-centered
cubic (BCC), face-centered cubic (FCC),
or hexagonal close-packed (HCP) crystals,
discussed in more detail in the Module 1,
Structure of Metals.
A face-centered
cubic crystal structure will deform more
readily under load before breaking than a
body-centered cubic structure.
The BCC lattice, although cubic, is not
closely packed and forms strong metals. a-iron and tungsten have the BCC form. The FCC
lattice is both cubic and closely packed and forms more ductile materials. g-iron, silver, gold, and
lead are FCC structured. Finally, HCP lattices are closely packed, but not cubic. HCP metals
like cobalt and zinc are not as ductile as the FCC metals.
Rev. 0
Page 9
MS-02