Test Instruments & Measuring Devices
AMMETERS
By Kirchhoff’s current law,
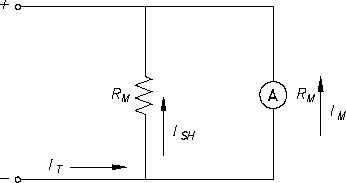
Figure 8 Ammeter with Shunt
ISH
IT
Im
Since the voltage across the shunt
must be equal to the voltage across
the ammeter, shunt resistance is
calculated as follows:
ISHRSH
ImRm
RSH
ImRm
ISH
RSH
ImRm
IT
Im
Therefore, the input resistance of a shunted ammeter is related to the meter and shunt resistance.
Equation (14-8) is a mathematical representation of this relationship.
NOTE: When computing accuracy for a shunted ammeter, use
.
R1m in place of Rm
(14-8)
R1m
RmRSH
Rm
RSH
Equation (14-9) is a mathematical representation of the relationship between input voltage and
current to the ammeter and the value of input resistance.
(14-9)
R1m
Vin
Iin
ImRm
IT
Example:
An ammeter, with a 100 W meter resistance and a full scale deflection current of
4 mA, is to be shunted to measure currents from 1 to 20 mA.
Find: 1.
RSH
2.
R1m
Rev. 0
Page 13
ES-14