FOUR BASIC ARITHMETIC OPERATIONS
Review of Introductory Mathematics
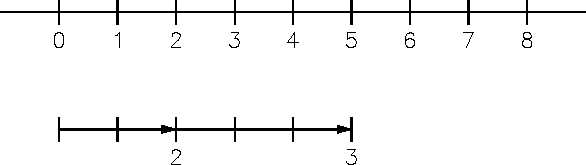
Starting at zero, we first move two places to the right on the number line to represent the number
2. We then move an additional 3 places to the right to represent the addition of the number 3.
The result corresponds to the position 5 on the number line. Using this very basic approach we
can see that 2 + 3 = 5. Two rules govern the addition of whole numbers.
The commutative law for addition states that two numbers may be added in either order
and the result is the same sum. In equation form we have:
a + b = b + a
(1-1)
For example, 5 + 3 = 8 OR 3 + 5 = 8. Numbers can be added in any order and
achieve the same sum.
The associative law for addition states that addends may be associated or combined in any
order and will result in the same sum. In equation form we have:
(a + b) + c = a + (b + c)
(1-2)
For example, the numbers 3, 5, and 7 can be grouped in any order and added to
achieve the same sum:
(3 + 5) + 7 = 15 OR 3 + (5 + 7) = 15
The sum of both operations is 15, but it is not reached the same way. The first
equation, (3 + 5) + 7 = 15, is actually done in the order (3 + 5) = 8. The 8 is
replaced in the formula, which is now 8 + 7 = 15.
The second equation is done in the order (5 + 7) = 12, then 3 + 12 = 15.
Addition can be done in any order, and the sum will be the same.
MA-01
Page 8
Rev. 0