COMPONENT ADDITION METHOD
Vectors
CP-02
Page 20
Rev. 0
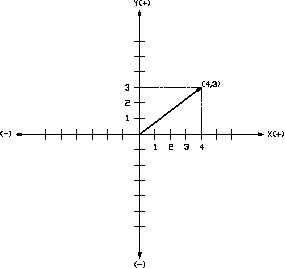
Figure 21 Vector Addition Component Method
COMPONENT ADDITION METHOD
Vector components are added along each axis to determine the magnitude and
direction of the resultant.
EO 1.3
ADD vectors using the following methods:
b.
Component addition
An Explanation of Components
The component addition method refers to the
addition of vector coordinates on a rectangular
(x,y) coordinate system. Coordinates, as seen
in previous examples, locate a specific point in
the system. Relative to vectors, that specific
point is the head of the vector. There are two
ways to locate that point. The head can be
located by counting the units along the x-axis
and the units along the y-axis, as illustrated in
Figure 21, where the point has coordinates
(4,3); i.e., the x component has a magnitude of
4 and the y component has a magnitude of 3.
The head can also be found by locating a vector
of the proper length on the positive side of the
x-axis, with its tail at the intersection of the x-
and y- axes. Then the vector is rotated a given
number of degrees in the counterclockwise direction. In this example, the head of the vector is
located five units at 36.9 . Five units is the length of the vector.
o
Using the Component Addition Method
To add vectors using the component addition method, use the following four step method.
Step 1.
Determine x- and y-axes components of all original vectors.
Step 2.
Mathematically combine all x-axis components.
Note: When combining, recognize that positive x components at 180 are equivalent
o
to negative x components at 0 (+x at 180 = -x at 0 ).
o
o
o