Thermodynamics
SECOND LAW OF THERMODYNAMICS
This calculation indicates that the Carnot cycle, operating with ideal components under real world
constraints, should convert almost 3/4 of the input heat into work. But, as will be shown, this
ideal efficiency is well beyond the present capabilities of any real systems.
Heat Rejection
To understand why an efficiency of 73% is not possible we must analyze the Carnot cycle, then
compare the cycle using real and ideal components. We will do this by looking at the T-s
diagrams of Carnot cycles using both real and ideal components.
The energy added to a working fluid during the Carnot isothermal expansion is given by qs. Not
all of this energy is available for use by the heat engine since a portion of it (qr) must be rejected
to the environment. This is given by:
qr = To Ds in units of Btu/lbm,
(1-37)
where To is the average heat sink temperature of 520°R. The available energy (A.E.) for the
Carnot cycle may be given as:
A.E. = qs - qr.
(1-38)
Substituting equation 1-37 for qr gives:
A.E. = qs - To Ds in units of Btu/lbm.
(1-39)
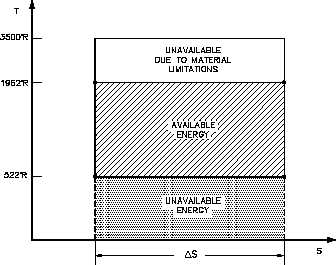
and is equal to the area of the shaded
Figure 28 Carnot Cycle
region labeled available energy in
Figure 28 between the temperatures
1962° and 520°R. From Figure 28 it
can been seen that any cycle operating
at a temperature of less than 1962°R
will be less efficient. Note that by
developing materials capable of
withstanding
the
stresses
above
1962°R, we could greatly add to the
energy available for use by the plant
cycle.
From equation 1-37, one can see why
the change in entropy can be defined
as a measure of the energy unavailable
to do work. If the temperature of the
heat sink is known, then the change in
entropy does correspond to a measure
of the heat rejected by the engine.
Rev. 0
Page 85
HT-01