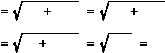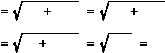TRIGONOMETRIC FUNCTIONS Trigonometry x      3 y      4 r   x²   y² 3²   4² r   9      16 25        5 Having solved for all three sides of the triangle, the trigonometric functions can now be determined.    Substitute  the  values  for  x,  y,  and  r  into  the  trigonometric  functions  and solve. sin  q   y r 4 5 0.800 cos  q   x r 3 5 0.600 tan  q   y x 4 3 1.333 csc  q   r y 5 4 1.250 sec  q   r x 5 3 1.667 cot  q   x y 3 4 0.750 Although  the trigonometric  functions  of  angles  are  defined  in  terms  of  lengths  of  the sides  of right  triangles,  they  are  really  functions  of  the  angles  only.     The  numerical  values  of  the trigonometric functions of any angle depend on the size of the angle and not on the length of the sides of the angle.   Thus, the sine of a 30 angle is always 1/2 or 0.500. Inverse  Trigonometric  Functions When the value of a trigonometric function of an angle is known,  the size of the angle can be found.    The  inverse  trigonometric  function,  also  known  as  the  arc  function,  defines  the  angle based on the value of the trigonometric function.   For example, the sine of 21 equals 0.35837; thus, the arc sine of 0.35837 is 21. MA-04 Page 6 Rev. 0