Trigonometry
TRIGONOMETRIC FUNCTIONS
(4-4)
tangent q
a
b
opposite
adjacent
(4-5)
cosecant q
c
b
hypotenuse
oposite
(4-6)
secant q
c
a
hypotenuse
adjacent
(4-7)
cotangent q
b
a
adjacent
opposite
The trigonometric value for any angle can be determined easily with the aid of a calculator. To
find the sine, cosine, or tangent of any angle, enter the value of the angle into the calculator and
press the desired function. Note that the secant, cosecant, and cotangent are the mathematical
inverse of the sine, cosine and tangent, respectively. Therefore, to determine the cotangent,
secant, or cosecant, first press the SIN, COS, or TAN key, then press the INV key.
Example:
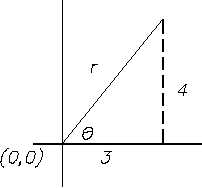
Determine the values of the six trigonometric functions of an angle formed by the x-axis
and a line connecting the origin and the point (3,4).
Solution:
To help to "see" the solution of the problem it helps to plot the points and construct the
right triangle.
Label all the known angles and sides, as shown in
Figure 3 Example Problem
Figure 3.
From the triangle, we can see that two of the sides
are known. But to answer the problem, all three
sides must be determined. Therefore the Pythagorean
theorem must be applied to solve for the unknown
side of the triangle.
Rev. 0
Page 5
MA-04