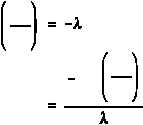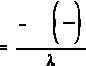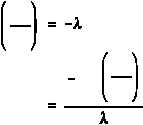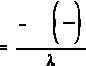A
Ao e
t
A
Ao e
t
A
Ao
e
t
ln
A
Ao
t
t
ln
A
Ao
t1/2
ln
1
2
t1/2
ln 2
0.693
RADIOACTIVITY
DOE-HDBK-1019/1-93
Atomic and Nuclear Physics
NP-01
Page 32
Rev. 0
Since the activity and the number of atoms are always proportional, they may be used
interchangeably to describe any given radionuclide population. Therefore, the following is true.
(1-5)
where:
A
=
activity present at time t
A
=
activity initially present
o
=
decay constant (time )
-1
t
=
time
Radioactive Half-Life
One of the most useful terms for estimating how quickly a nuclide will decay is the radioactive
half-life. The radioactive half-life is defined as the amount of time required for the activity to
decrease to one-half of its original value. A relationship between the half-life and decay constant
can be developed from Equation (1-5). The half-life can be calculated by solving Equation (1-5)
for the time, t, when the current activity, A, equals one-half the initial activity A .o
First, solve Equation (1-5) for t.
If A is equal to one-half of A , then A/A is equal to one-half. Substituting this in the equation
o
o
above yields an expression for t .
1/2
(1-6)