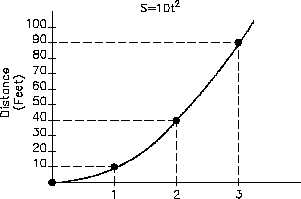
CALCULUS Higher Concepts of Mathematics The instantaneous velocity again equals the Figure 5    Graph of Distance vs. Time value of the derivative  ds/dt.   This value is changing    with    time. However,    the instantaneous velocity at any specified time can be determined.   First, small changes in s and t are considered. Ds Dt (s Ds) s (t Dt) t The values of (s + Ds) and s in terms of (t  +  Dt) and  t  using Equation 5-5, can then be substituted into this expression.   At time t,  s  =  10t²;  at  time  t  +  Dt,  s  +  Ds  =  10(t  + Dt)².    The  value  of  (t  +  Dt)²  equals  t²  + 2t(Dt)   +   (Dt)²;   however,   for   incremental values  of  Dt,  the  term  (Dt)²  is  so  small,  it can  be  neglected.    Thus,  (t  +  Dt)²  =  t²  + 2t(Dt). Ds Dt 10[t² 2t(Dt)] 10t² (t Dt) t Ds Dt 10t² 20t(Dt)] 10t² t Dt t Figure 6    Slope of a Curve Ds Dt 20t The  value  of  the  derivative  ds/dt  in  the  case plotted in Figure 5 equals 20t.   Thus, at time t = 1 s,  the  instantaneous  velocity  equals  20 ft/s;  at  time  t  =  2  s,  the  velocity  equals  40 ft/s, and so on. When the graph of a function is not a straight line,   the   slope   of   the   plot   is   different   at different points.   The slope of a curve at any point is defined   as the slope of a line drawn tangent  to  the  curve  at  that  point.    Figure  6 shows  a  line  drawn  tangent  to  a  curve.    A tangent line is a line that touches the curve at only one point.   The line AB is tangent to the MA-05 Page 36 Rev. 0