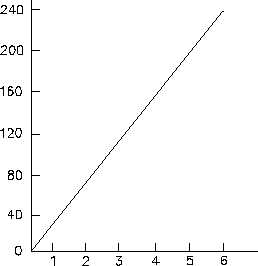
Higher Concepts of Mathematics CALCULUS The value of the derivative ds/dt for the case Figure 4    Graph of Distance vs. Time plotted  in  Figure  4  can  be  understood  by considering small changes in the two variables s and t. Ds Dt (s Ds) s (t Dt) t The values of (s + Ds) and s in terms of (t + Dt)  and  t,  using  Equation  5-4  can  now  be substituted into this expression.   At time  t,  s = 40t; at time t + Dt, s + Ds = 40(t + Dt). Ds Dt 40(t Dt) 40t (t Dt) t Ds Dt 40t 40(Dt) 40t t Dt t Ds Dt 40(Dt) Dt Ds Dt 40 The value of the derivative ds/dt in the case plotted in Figure 4 is a constant.   It equals 40 ft/s. In the discussion of graphing, the slope of a straight line on a graph was defined as the change in y, Dy, divided by the change in x, Dx.  The slope of the line in Figure 4 is Ds/Dt which, in this case,  is  the  value  of  the  derivative  ds/dt.   Thus,  derivatives  of  functions  can  be  interpreted  in terms of the slope of the graphical plot of the function.   Since the velocity equals the derivative of the distance s with respect to time t, ds/dt, and since this derivative equals the slope of the plot of  distance  versus  time,  the  velocity  can  be  visualized  as  the  slope  of  the  graphical  plot  of distance versus time. For  the  case  shown  in  Figure  4,  the  velocity  is  constant.    Figure  5  is  another  graph  of  the distance traveled by an object as a function of the elapsed time.   In this case the velocity is not constant.   The functional relationship shown is given by the following equation: s = 10t² (5-5) Rev. 0 Page 35 MA-05