vp
2 k T
m
vp
2 k T
m
2
1.38 x 1016erg
K
293 K
1.66 x 1024 g
2.2 x 105cm
sec
1 m
100 cm
2200
m
sec
Reactor Theory (Neutron Characteristics)
DOE-HDBK-1019/1-93
NEUTRON FLUX SPECTRUM
Rev. 0
Page 35
NP-02
In the thermal region the neutrons achieve a thermal equilibrium with the atoms of the moderator
material. In any given collision they may gain or lose energy, and over successive collisions
will gain as much energy as they lose. These thermal neutrons, even at a specific temperature,
do not all have the same energy or velocity; there is a distribution of energies, usually referred
to as the Maxwell distribution (e.g., Figure 2). The energies of most thermal neutrons lie close
to the most probable energy, but there is a spread of neutrons above and below this value.
Most Probable Neutron Velocities
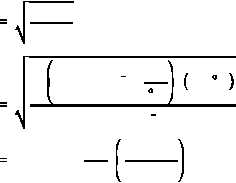
The most probable velocity (v ) of a thermal neutron is determined by the temperature of the
p
medium and can be determined by Equation (2-13) .
(2-13)
where:
v
=
most probable velocity of neutron (cm/sec)
p
k
=
Boltzman's constant (1.38 x 10
erg/ K)
-16
T
=
absolute temperature in degrees Kelvin ( K)
m =
mass of neutron (1.66 x 10
grams)
-24
Example:
Calculate the most probable velocities for neutrons in thermal equilibrium with their
surroundings at the following temperatures. a) 20 C, b) 260 C.
Solution:
a)
Calculate the most probable velocity for 20 C using Equation (2-13).