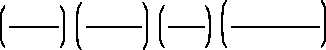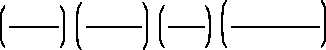mgz
gc
PE
mgz
gc
50 lbm
1
32.17 ft
sec2
10 ft
1
lbf sec2
32.17 lbm ft
KE
mv2
2gc
ENERGY AND WORK
Energy, Work, and Power
CP-05
Page 2
Rev. 0
As an example, consider the energy stored in hydrogen and oxygen as potential energy to be
released on burning. Burning changes their relative separation distance from the elemental form
to the compound form as water releases the potential energy.
When discussing mechanical potential energy, we look at the position of an object. The
measure of an object's position is its vertical distance above a reference point. The reference
point is normally the earth's surface, but can it be any point. The potential energy of the object
represents the work required to elevate the object to that position from the reference point.
Potential energy is mathematically represented by Equation 5-1.
PE = work to elevate = weight x height
(5-1)
where:
PE
=
potential energy in ft-lbf
m
=
mass in lbm
g
=
32.17 ft/sec2
g
=
32.17 (lbm-ft)/(lbf-sec )
c
2
z
=
height above a reference in ft
It should be noted the g is used only when using the English system of measurement.
c
Example:
What is the potential energy of a 50 lbm object suspended 10 feet above the
ground?
Answer:
PE = 500 ft-lbf
Kinetic Energy
Kinetic energy is defined as the energy stored in an object because of its motion. If you have
a baseball in your hand, it has no kinetic energy because it is not moving. But if you throw the
ball, your hand has provided energy to give the ball motion. When you release the ball, it leaves
your hand at some velocity. The energy you have given the ball will determine the velocity of
the ball. Because the kinetic energy is due to the motion of the object, and motion is measured
by velocity, kinetic energy can be calculated in terms of its velocity, as shown below.
(5-2)