FM
µs N
FK
µK N
Application of Newton's Laws
TYPES OF FORCE
Rev. 0
Page 19
CP-04
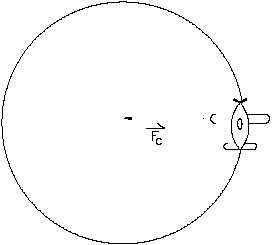
Figure 10 Centripetal Force
Experimental evidence shows that the maximum value F of the static-friction force is
M
proportional to the normal component N of the reaction of the surface, as shown in Equation
4-5.
(4-5)
The term µ is a constant called the coefficient of static friction. Similarly, the magnitude F of
s
K
the kinetic-friction force may be expressed in the following form.
(4-6)
The term µ is a constant called the coefficient of kinetic friction. The coefficients of friction,
K
µ and µ , do not depend upon the area of the surfaces in contact. Both coefficients, however,
S
K
depend strongly on the nature of the surfaces in contact. Since they also depend upon the exact
condition of the surfaces, their value is seldom known with an accuracy greater than 5 percent.
It should be noted that frictional forces are always opposite in direction to the motion (or
impending motion) of the object.
Centripetal Force
An object moving at constant speed in a circle
is not in equilibrium. Although the magnitude
of the linear velocity is not changing, the
direction of velocity is continually changing.
Since a change in direction requires
acceleration, an object moving in a circular
path has a constant acceleration towards the
center of the circular path.
Recalling Newton's second law of motion, F =
ma, a force is required to cause acceleration.
Therefore, to have constant acceleration towards
the center of the circular path, there must be a net
force acting towards the center. This force is
known as centripetal force. Without this force, an
object will move in a straight line. Figure 10
illustrates the centripetal force.